
Bài toán con Ngựa đi tuần (quân Mã đi tuần trong bàn cờ vua) là một bài toán cực kỳ thú vị, phù hợp với cả các bé nhỏ tuổi đến cả người lớn. Các bạn có thể giải bài toán này để thư giãn và phát triển khả năng hình học, phát triển khả năng sáng tạo cho các bé.
Đề bài: Trong một bàn cờ vua, bằng cách nào mà con Ngựa (quân Mã) có thể đi tuần hết tất cả các ô trên bàn cờ vua và quay về lại vị trí ban đầu. Trong đó, mỗi ô chỉ đi 1 lần (trừ ô bắt đầu cũng là ô kết thúc đi tuần).
Bạn hãy dành ít phút để tự suy nghĩ lời giải cho bài toán trên trước khi xem lời giải nhé.
Lời giải của bài toán:
Có nhiều lời giải cho bài toán con Ngựa đi tuần (quân Mã đi tuần). Tuy nhiên, trong đó có những lời giải thiên về số học, toán cao cấp,… chỉ thích hợp cho các bạn theo chuyên ngành Toán và về thực tế dể gây nhàm chán và không giúp các bé có thêm niềm yêu thích toán học. Do đó, xin giới thiệu cách bằng Phương pháp sử dụng hình ảnh dể hiểu, đơn giản, thủ công nhưng giúp bạn và các bé khơi nguồn cảm xúc sáng tạo cũng như thư giãn hơn các cách giải trên.
Bước 1: Hãy vẽ bàn cờ vua 64 ô (8 hàng ngang x8 hàng dọc)

Bước 2: Chọn ngẫu nhiên điểm bắt đầu đi tuần của quân Mã, nên chọn 1 trong 4 ô góc.
Lời giải này chọn ô bắt đầu là A8 ( đánh dấu bằng logo nhatrang chess)

Bước 3: Vẽ đường đi của quân Mã từ điểm bắt đầu. Cố gắng vẽ đường đi đến nhiều ô (không trùng) nhất có thể. Tất cả các ô còn lại mà quân Mã chưa đi tuần, các bạn hãy nối đường đi riêng lẻ lại với nhau (tất nhiên vẫn theo quy tắc cách đi của quân Mã trên bàn cờ vua). Sau khi hoàn thành, trên bàn cờ vua có 1 đường đi chính, dài nhất và có thể có nhiều đoạn đường đi riêng lẻ.
Ví dụ: sau khi nối đường đi của quân Mã giữa tất cả các ô thì có 2 ô bị cụt đường như hình dưới
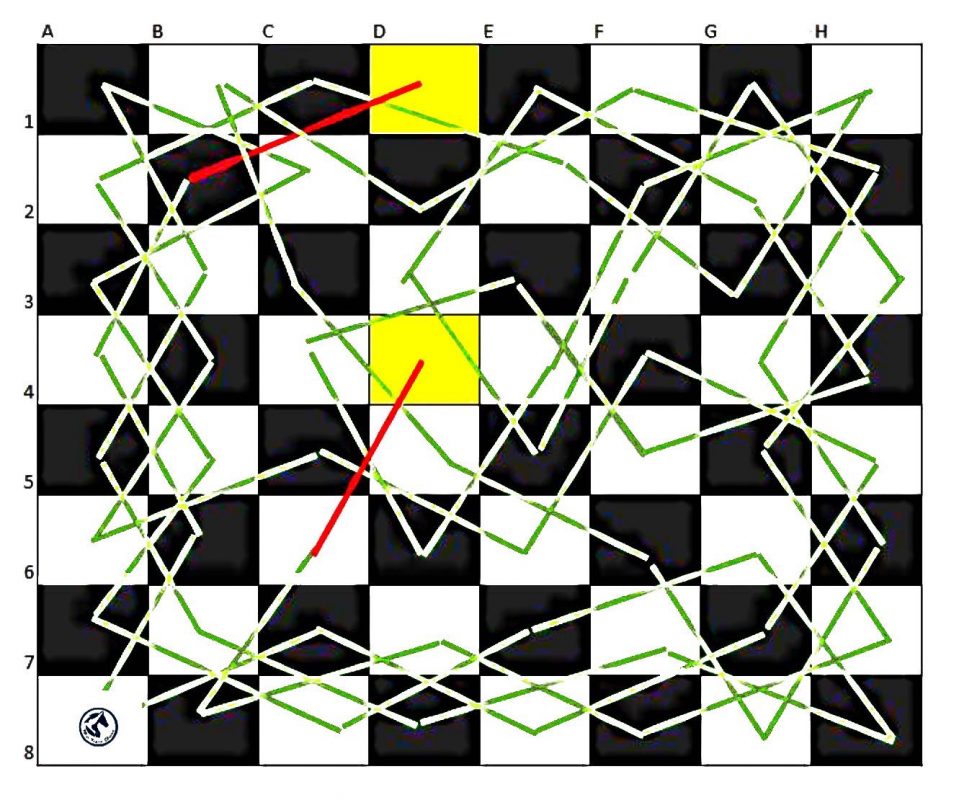
Bước 4: Cắt đường đi cũ, nối với các khúc đường đi riêng lẻ. Thực hiện liên tục cho đến khi có được 1 đường đi duy nhất. Đến đây, bạn đã giải được bài toán.
Các bạn thực hiện thay đổi đường đi, bỏ đường đi cũ (đường màu vàng), thêm đường đi mới (đường màu xanh da trời) để được đường đi hoàn chỉnh. Chịu khó quan sát và thực hiện vài lần là sẽ thực hiện được.
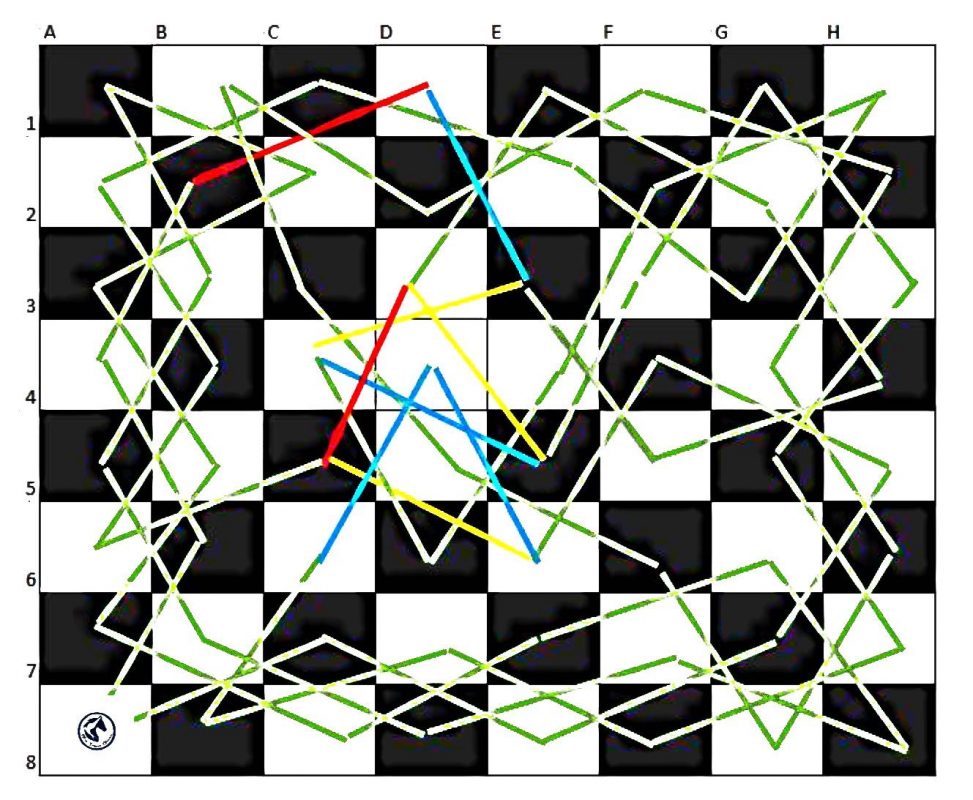
Có rất nhiều cách đi để giải được bài toán trên. Phía dưới đây là một lời giải hoàn chỉnh cho bài toán con Ngựa đi tuần (quân Mã đi tuần). Các bạn có thể thử kiểm tra lại đường đi đã đi đến tất cả các ô, chỉ đi 1 lần qua mỗi ô sau đó về lại điểm bắt đầu là đúng.
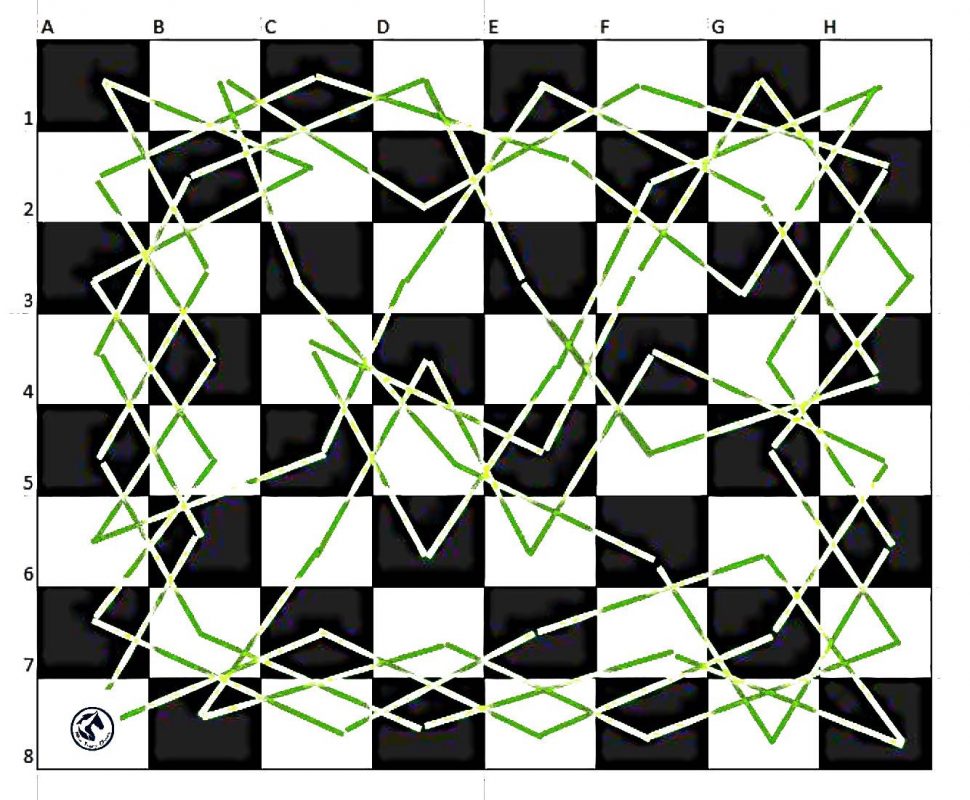
Biết thêm về bài toán:
Quân mã được đặt ở một ô trên một bàn cờ trống nó phải di chuyển theo quy tắc của cờ vua để đi qua mỗi ô trên bàn cờ đúng một lần. Có rất nhiều lời giải cho bài toán này, chính xác là 26.534.728.821.064 lời giải trong đó quân mã có thể kết thúc tại chính ô mà nó khởi đầu.
Một hành trình như vậy được gọi là hành trình đóng. Có những hành trình, trong đó quân mã sau khi đi hết tất cả 64 ô của bàn cờ (kể cả ô xuất phát), thì từ ô cuối của hành trình không thể đi về ô xuất phát chỉ bằng một nước đi. Những hành trình như vậy được gọi là hành trình mở.
Nhiều biến thể của chủ đề này được các nhà toán học nghiên cứu, trong đó có nhà toán học Euler. Các biến đổi có thể theo các hướng: thay đổi kích thước bàn cờ, biến thành trò chơi hai người theo tư tưởng này, giảm nhẹ các yêu cầu trên đường đi của quân mã.
Bài toán mã đi tuần là một dạng của bài toán tổng quát hơn là bài toán tìm đường đi Hamilton trong lý thuyết đồ thị, là một bài toán NP-đầy đủ. Bài toán tìm hành trình đóng của quân mã là một bài toán cụ thể của bài toán tìm chu trình hamiltonian.
Hành trình của quân mã trên nửa bàn cờ đã được giới thiệu dưới dạng thơ trong một tác phẩm tiếng Phạn.
Giải thuật đầu tiên đầy đủ cho bài toán về hành trình của quân mã là Giải thuật Warnsdorff, công bố lần đầu năm 1823 bởi H. C. Warnsdorff.
ST.

